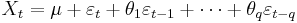Moving-average model
In time series analysis, the moving-average (MA) model is a common approach for modeling univariate time series models. The notation MA(q) refers to the moving average model of order q:
where μ is the mean of the series, the θ1, ..., θq are the parameters of the model and the εt, εt−1,... are white noise error terms. The value of q is called the order of the MA model.
That is, a moving-average model is conceptually a linear regression of the current value of the series against previous (unobserved) white noise error terms or random shocks. The random shocks at each point are assumed to come from the same distribution, typically a normal distribution, with location at zero and constant scale. The distinction in this model is that these random shocks are propagated to future values of the time series. Fitting the MA estimates is more complicated than with autoregressive models (AR models) because the error terms are not observable. This means that iterative non-linear fitting procedures need to be used in place of linear least squares. MA models also have a less obvious interpretation than AR models.
Sometimes the autocorrelation function (ACF) and partial autocorrelation function (PACF) will suggest that a MA model would be a better model choice and sometimes both AR and MA terms should be used in the same model (see Box-Jenkins).
Note, however, that the error terms after the model is fit should be independent and follow the standard assumptions for a univariate process: random drawings from a fixed distribution with the distribution having fixed location and with the distribution having fixed variation.
The moving-average model is essentially a finite impulse response filter with some additional interpretation placed on it.
See also
External links
This article incorporates public domain material from websites or documents of the National Institute of Standards and Technology.